Fermat's Theorem

Fermat’s Theorem: Supposse a function which it's defined on the interval (a, b), in which we can find c. 

If f(c) is an extreme value of f, and f is differentiable at c, then f’(c) = 0.

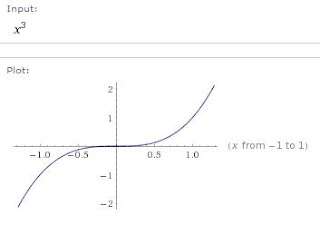
A maximum or minimum can occur where the derivative doesn't exist. And also, a point where the derivative is zero may not be a maximum or minimum point. For example, a function that increases, has a region with slope equals to 0 and continues increasing. It's not an extremum value. 

The second derivative

The derivative measures how changes to the input affect the output. The second derivative measures how the derivative is changing. The sign of the second derivative measures concavity.

Concave up: f’’ > 0

Concave down: f’’ < 0

The point between concave up and concave down, where the second derivative is equal to 0, is called an inflection point.